Fuzzy cognitive mapping might give you quite a cultural shock if you come from a qualitative cognitive mapping background (for a comparison see also [2]). This is even more so when being confronted with phrases such as fuzzy logic, sigmoid squashing function or machine learning algorithms. But do not worry.
The most notable difference is that you assign numbers to statements and links. These numbers are usually in percentage terms. This is essentially the fuzzy part because statements and links now express degrees of belief. Another difference is that your cognitive map becomes dynamic. That means the link values determine how much value the connected statements exchange. When you calculate this exchange, the statement values may increase or decrease. You can calculate the exchange again, and may get new statement values, etc.
Figure 1 Fuzzy cognitive maps; generic example
On top of figure 1 you see the initial state of a fuzzy cognitive map. The statements are named according to their initial values for illustrative purposes. Normally they are named after that what they model. The exchange between two statements 1 -> 2 is only determined by the "recipient" of a connection. That means 1 would not change its value, only 2. 2's new value would be the value of 1 times the value of the link from 1 to 2 in percent. Notice that values do not accumulate through the iterations.
With that knowledge in mind, work through figure 1 and confirm the value changes yourself.
Statement weights
The weights of statements usually range between 0 and 1 or -1 and 1. The range you choose depends on what you actually model and particularly how you interpret the meaning of your fuzzy cognitive map.
In [1] (p156), for instance, they suggest a decision-making analogy. According to them you have two options. Using the range [0,1] means that if you have two statements, one with a score of 0 and the other one with a score of 1, the former will correspond to the wrong decision and latter to the right one. A value of 0.5 would be the middle and mean maximum uncertainty.
The range [-1,1] in contrast allows you to express a decision to be right or wrong within the statement where -1 means that particular statement is wrong and 1 means that particular statement is right. A value of 0 would be the middle.
Notice that you have to assign initial values for each statement yourself.
Also notice that if a statement has no in-linking statements, it will obtain 0 as a value after the first calculation. The absence of in-linking statements means the statement in focus receives 0 as new value. To avoid that, you can hold the initial value constant [3].
Finally notice that different terms are used for "statement" in the literature such as nodes or vertices.
Link weights
The weights of links usually are expressed in percentage terms from -1 to 1 where 1 means absolute certainty that A causes B and -1 means absolute certainty that A causes not B. 0 means no causal relationship, i.e. no link at all.
Notice that different terms are used for "link" in the literature such as edges, arrows or arcs.
An error in figure 1
You may have noticed that figure 1 shows values greater than 1. In order to contain the statement values within the desired interval, squashing functions are used. You calculate the statement values as outlined above and then feed the result into a squashing function. The choice of the function depends on the desired range of your statements. Be aware that many of the functions recommended are only approximations. The sigmoid function, for instance, is never equal to 0 or 1.
Graphical and tabular representation of a fuzzy cognitive map
You will likely encounter another form of representation of a fuzzy cognitive map. It looks like a table and is called a matrix. You read the matrices from left to top.
Figure 2 Graph on the left is the same as the matrix on the right
An equation
This equation ([1], p156) captures the steps discussed above. Aj is the statement in focus. Ai is each in-linking statement to Aj. W is the link value from each Ai to Aj. The t-1 in Ai might be a bit confusing. It means the value of Ai of the previous iteration. Instead, you can also write t+1 in Aj. It is the value of Aj for the next iteration.
The index numbers i and j refer to the matrix. The big sigma tells you to go over each matrix pair or table cell. Imagine that you count from 1 to 3 twice in the following way:
1: 1, 2, 3
2: 1, 2, 3
3: 1, 2, 3
If you replace the numbers with statement names, here A, B, C, you will compare each statement to all other statements.
A: A, B, C
B: A, B, C
C: A, B, C
Or expressed in individual comparisons: A->A, A->B, A->C, etc. Notice however that i≠j hence you skip A->A, B->B, C->C.
Do not forget the f(). The value of the sum is feed into the squashing function. This is the sigmoid squashing function for instance:
"where Lambda is a real number" [4]
Are link values fixed?
Yes, in the "classical" use of fuzzy cognitive mapping, they are. However, for further readings you may want to look into machine learning algorithms. The basic gist of these is that the weights of links change as well.
References
[1] Stylios, C. D. and Groumpos, P. P. (2004) "Modeling Complex Systems Using Fuzzy Cognitive Maps", IEEE TRANSACTIONS ON SYSTEMS, MAN, AND CYBERNETICS—PART A: SYSTEMS AND HUMANS, VOL. 34, NO. 1, JANUARY 2004, pp. 155-162.
[2] http://causal-cognitive-mapping.blogspot.de/2017/05/the-different-types-of-cognitive-mapping.html
[3] http://edepot.wur.nl/290911
[4] http://related-to-programming-and-maths.blogspot.de/2017/05/where-lambda-is-real-number.html



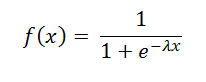
No comments:
Post a Comment
Use the select box below and choose "Anonymous" if you wish to comment as guest.